Математические фигуры окружают нас с первых лет жизни. Крыша дома напоминает треугольник, окно — квадрат, а солнце — круг. При этом далеко не все догадываются, что равнобедренный треугольник обладает уникальными свойствами, которые делают его особенным среди других геометрических фигур. Две равные стороны создают симметрию, а углы при основании всегда одинаковы — это закон, который работает безотказно.
Детский ум легко схватывает простые правила, однако взрослые часто забывают элементарные вещи. Школьники второго класса без труда называют признаки квадрата, тогда как выпускники вузов иногда путаются в базовых формулах. Парадокс заключается в том, что сложность математики растет не от количества формул, а от неумения применять простые принципы на практике.
Геометрические задачи встречаются повсеместно — от расчета материалов для ремонта до проектирования садового участка. Знание того, как найти периметр квадрата, поможет определить количество досок для забора или длину бордюра вокруг клумбы. Эти навыки становятся особенно ценными, когда теория превращается в практическое применение.
Математическая элегантность равнобедренных фигур
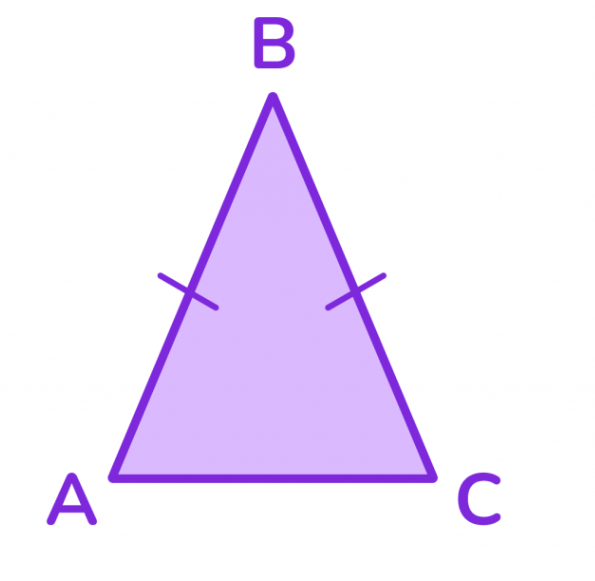
Природа равнобедренного треугольника кроется в его симметрии. Боковыми называются равные стороны, а третья сторона — основанием, что создает идеальный баланс формы. Такая конструкция встречается в архитектуре древних пирамид, современных мостах и даже в листьях деревьев.
Уникальность этой фигуры проявляется в математических свойствах. Углы при основании всегда равны, что превращает каждый равнобедренный треугольник в предсказуемую структуру. Высота, опущенная на основание, одновременно становится медианой и биссектрисой — три функции в одной линии.
Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника. Это свойство открывает путь к многочисленным вычислениям через теорему Пифагора. Практическое значение такого подхода сложно переоценить — от расчета стропильной системы до определения углов наклона солнечных панелей.
 Периметр квадрата: простота в деталях
Периметр квадрата: простота в деталях
Квадрат представляет собой геометрическое совершенство — четыре равные стороны и четыре прямых угла. Чтобы посчитать периметр квадрата, можно сложить длины всех сторон, либо умножить длину одной его стороны на четыре. Формула P = 4a выглядит обманчиво просто, однако за ней скрывается множество практических применений.
У квадрата все стороны равны. Периметр квадрата равен сумме длин всех сторон квадрата, что делает вычисления максимально понятными даже для младших школьников. Однако важность этого навыка выходит далеко за рамки учебных задач — строители используют его для расчета материалов, дизайнеры — для планирования пространства, а садоводы — для разметки участков.
Математические принципы работают независимо от масштаба: будь то квадратный сантиметр на чертеже или квадратный километр на карте. Это универсальность формулы превращает простое умножение в мощный инструмент для решения реальных задач.
Тетрика: персональный подход к математическому образованию
Современное образование требует индивидуального подхода, особенно в изучении точных наук. Онлайн-школа Тетрика предлагает персонализированные занятия с репетиторами, которые адаптируют программу под конкретного ученика. Такой метод позволяет устранить пробелы в знаниях и развить математическое мышление без стресса и принуждения.
Квалифицированные преподаватели школы понимают: геометрия становится понятной, когда теория подкрепляется практическими примерами. Равнобедренные треугольники перестают быть абстракцией, превращаясь в реальные объекты — от шоколадных долек до архитектурных элементов. А формулы периметра квадрата обретают смысл через бытовые задачи.
Персональные занятия с репетитором дают возможность задавать любые вопросы и получать развернутые объяснения. Ученик движется в собственном темпе, закрепляя каждую тему до полного понимания. Результат такого подхода — не механическое заучивание формул, а глубокое понимание математических принципов, которые пригодятся в жизни.
Интерактивные методы обучения в Тетрике превращают изучение математики в увлекательный процесс. Визуализация задач, практические упражнения и индивидуальная обратная связь создают оптимальные условия для усвоения материала. Школьники начинают видеть красоту в математических закономерностях и применять полученные знания с уверенностью.